Standard Position Of An Angle

1.ane: Angles

1. Last updated

2. Salve as PDF

Folio ID

59541

Learning Objectives

• Describe angles in standard position.
• Convert betwixt degrees and radians.
• Detect coterminal angles.
• Notice the length of a round arc.
• Detect the surface area of a sector of a circle

A golfer swings to hit a ball over a sand trap and onto the green. An airline airplane pilot maneuvers a aeroplane toward a narrow runway. A dress designer creates the latest manner. What exercise they all have in common? They all work with angles, then practice all of usa at once or another. Sometimes we demand to mensurate angles exactly with instruments. Other times we judge them or judge them by heart. Either way, the proper angle can make the deviation between success and failure in many undertakings. In this section, we volition examine properties of angles.

Drawing Angles in Standard Position

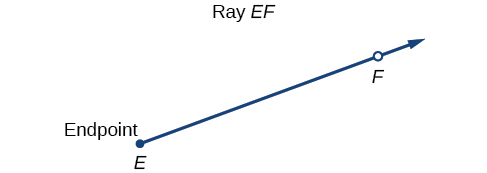
Properly defining an angle first requires that we define a ray. A ray consists of ane betoken on a line and all points extending in one direction from that point. The showtime point is called the endpoint of the ray. We tin refer to a specific ray by stating its endpoint and any other point on it. The ray in Effigy \(\PageIndex{ane}\) can exist named as ray EF, or in symbol form \(\overrightarrow{EF}\).

Figure \(\PageIndex{1}\)

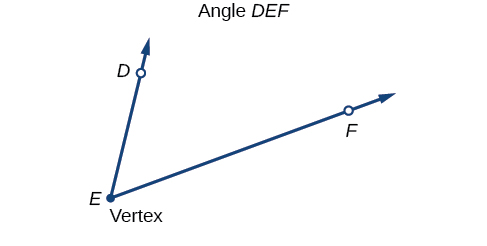
An angle is the union of two rays having a mutual endpoint. The endpoint is called the vertex of the bending, and the two rays are the sides of the angle. The angle in Figure \(\PageIndex{2}\) is formed from \(\overrightarrow{ED}\) and \(\overrightarrow{EF}\). Angles tin be named using a point on each ray and the vertex, such as angle DEF, or in symbol form \(∠DEF.\)

Figure \(\PageIndex{2}\)

Greek letters are often used equally variables for the measure of an angle. Table \(\PageIndex{1}\) is a listing of Greek letters commonly used to represent angles, and a sample angle is shown in Figure \(\PageIndex{3}\).

Table \(\PageIndex{i}\)

\(θ\)	\(φ \text{ or }ϕ\)	\(α\)	\(β\)	\(γ\)
theta	phi	alpha	beta	gamma

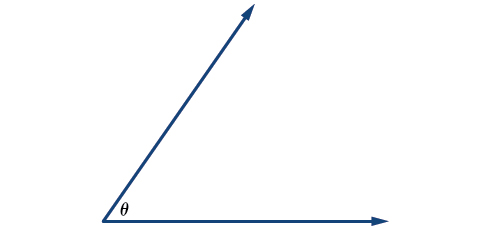
Figure \(\PageIndex{3}\): Angle theta, shown as \(∠θ\)

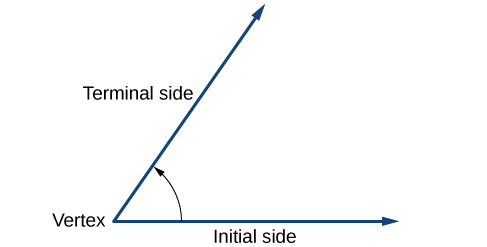
Angle creation is a dynamic process. We start with two rays lying on pinnacle of ane another. We leave 1 fixed in identify, and rotate the other. The fixed ray is the initial side , and the rotated ray is the final side. In order to identify the different sides, we bespeak the rotation with a small arc and pointer shut to the vertex as in Figure \(\PageIndex{iv}\).

Figure \(\PageIndex{4}\)

Equally we discussed at the offset of the section, at that place are many applications for angles, but in order to employ them correctly, we must be able to measure them. The mensurate of an angle is the amount of rotation from the initial side to the terminal side. Probably the most familiar unit of angle measurement is the degree. One degree is \(\frac{1}{360}\) of a circular rotation, so a complete circular rotation contains 360 degrees. An angle measured in degrees should always include the unit of measurement "degrees" afterwards the number, or include the degree symbol °. For example, 90 degrees = 90°.

To formalize our work, we will begin by cartoon angles on an 10-y coordinate airplane. Angles can occur in any position on the coordinate plane, but for the purpose of comparison, the convention is to illustrate them in the same position whenever possible. An angle is in standard position if its vertex is located at the origin, and its initial side extends along the positive x-axis. See Figure \(\PageIndex{5}\).

Effigy \(\PageIndex{5}\)

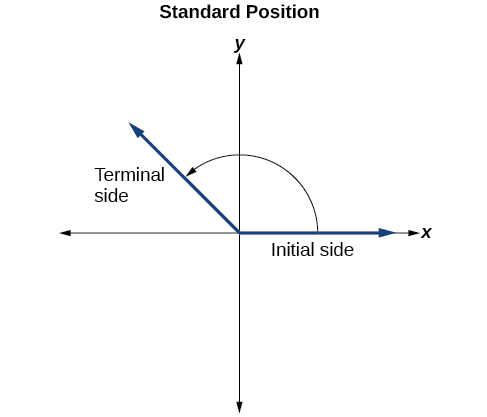
If the angle is measured in a counterclockwise direction from the initial side to the terminal side, the angle is said to be a positive angle. If the angle is measured in a clockwise management, the bending is said to exist a negative bending.

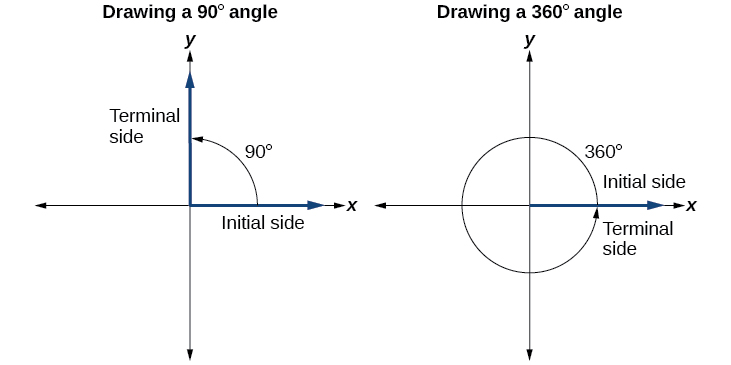
Drawing an bending in standard position always starts the same way—draw the initial side along the positive ten-centrality. To place the terminal side of the angle, nosotros must calculate the fraction of a total rotation the angle represents. We do that by dividing the angle measure in degrees by 360°. For example, to draw a 90° angle, we calculate that \(\frac{90°}{360°}=\frac{1}{four}\). So, the terminal side will be ane-fourth of the manner around the circle, moving counterclockwise from the positive x-axis. To draw a 360° angle, nosotros calculate that \(\frac{360°}{360°}=1\). So the terminal side will be 1 consummate rotation effectually the circle, moving counterclockwise from the positive x-centrality. In this case, the initial side and the terminal side overlap. Come across Figure \(\PageIndex{6}\) .

Figure \(\PageIndex{6}\)

Since we define an angle in standard position by its initial side, we accept a special blazon of bending whose terminal side lies on an axis, a quadrantal angle. This type of bending can have a mensurate of 0°, 90°, 180°, 270° or 360°. See Figure \(\PageIndex{7}\).

Effigy \(\PageIndex{seven}\): Quadrantal angles are angles in standard position whose terminal side lies along an centrality. Examples are shown.

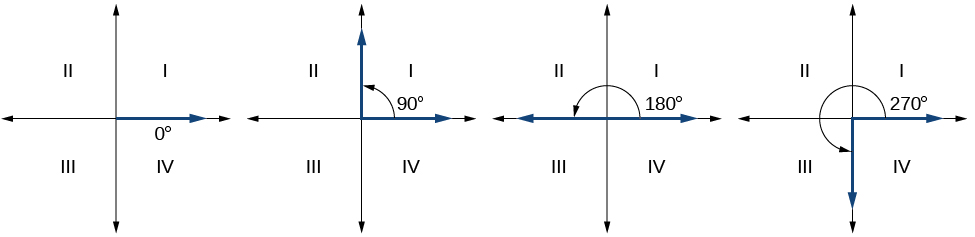
QUADRANTAL ANGLES

Quadrantal angles are angles in standard position whose concluding side lies on an axis, including 0°, ninety°, 180°, 270°, or 360°.

Given an angle measure in degrees, draw the angle in standard position

1. Limited the angle mensurate every bit a fraction of 360°.
2. Reduce the fraction to simplest grade.
3. Draw an angle that contains that same fraction of the circle, beginning on the positive x-axis and moving counterclockwise for positive angles and clockwise for negative angles.

Example \(\PageIndex{1}\): Drawing an Angle in Standard Position Measured in Degrees

1. Sketch an angle of thirty° in standard position.
2. Sketch an angle of −135° in standard position.

Solution

1. Split up the angle measure past 360°.

   \[\dfrac{30°}{360°}=\dfrac{1}{12}\]

   To rewrite the fraction in a more familiar fraction, we can recognize that

   \[\dfrac{i}{12}=\dfrac{one}{3}(\frac{1}{4})\]

   I-twelfth equals one-third of a quarter, then by dividing a quarter rotation into thirds, nosotros tin can sketch a line at 30° as in Figure \(\PageIndex{viii}\).
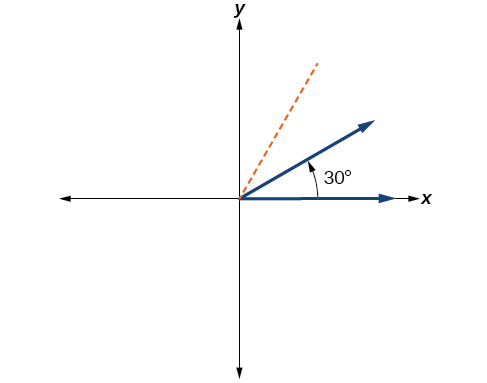
   Effigy \(\PageIndex{eight}\)

2. Separate the angle measure by 360°.

   \[\dfrac{−135°}{360°}=−\dfrac{three}{8}\]

   In this case, we can recognize that

   \[−\dfrac{three}{8}=−\dfrac{iii}{2}(\dfrac{1}{4})\]

   Negative three-eighths is i and 1-half times a quarter, so nosotros place a line by moving clockwise one total quarter and one-half of some other quarter, every bit in Figure \(\PageIndex{9}\).
   
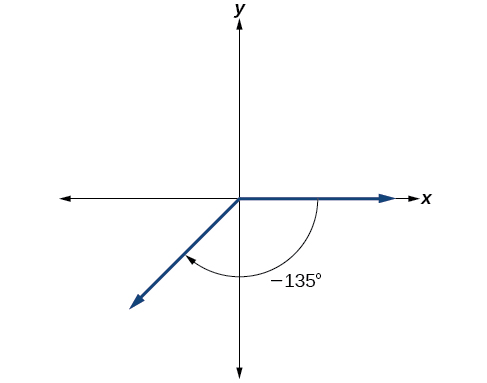
   Figure \(\PageIndex{9}\)

\(\PageIndex{one}\):

Testify an bending of 240° on a circle in standard position.

Solution

Effigy \(\PageIndex{10}\)

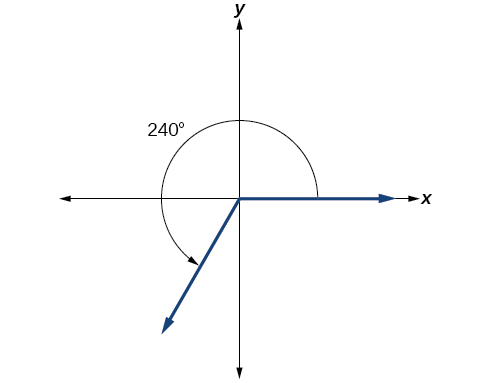
Converting Betwixt Degrees and Radians

Dividing a circle into 360 parts is an capricious choice, although it creates the familiar caste measurement. We may choose other ways to dissever a circumvolve. To find another unit, retrieve of the procedure of drawing a circle. Imagine that you end earlier the circle is completed. The portion that you drew is referred to every bit an arc. An arc may be a portion of a full circle, a full circumvolve, or more than a total circle, represented past more than 1 full rotation. The length of the arc effectually an entire circle is called the circumference of that circumvolve.

The circumference of a circle is \(C=2πr\). If we divide both sides of this equation by \(r\), nosotros create the ratio of the circumference to the radius, which is ever \(2π\) regardless of the length of the radius. And so the circumference of whatsoever circle is \(2π≈half-dozen.28\) times the length of the radius. That ways that if we took a cord every bit long as the radius and used it to mensurate consecutive lengths effectually the circumference, there would be room for vi full string-lengths and a little more than than a quarter of a seventh, as shown in Figure \(\PageIndex{11}\).

Figure \(\PageIndex{xi}\)

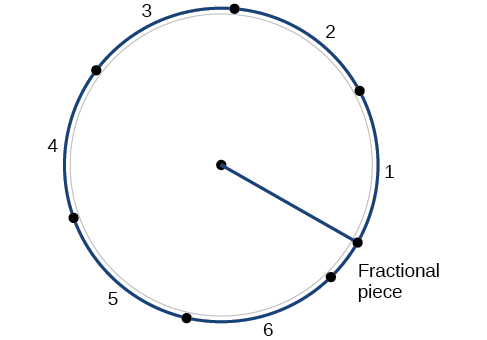
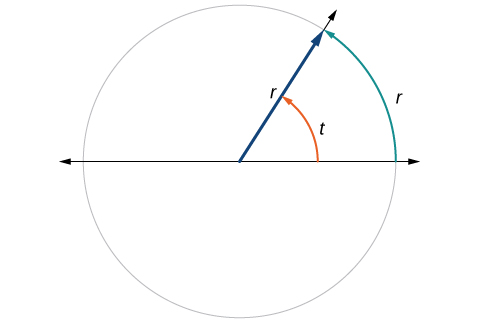
This brings us to our new angle measure out. One radian is the measure of a central angle of a circumvolve that intercepts an arc equal in length to the radius of that circle. A central angle is an angle formed at the center of a circle by two radii. Because the total circumference equals \(2π\) times the radius, a full circular rotation is \(2π\) radians. Then

\[\begin{align} 2π \text{ radians } & =360^∘ \\ π \text{ radians } & =\dfrac{360^∘}{2}=180^∘ \\ 1 \text{ radian } & =\dfrac{180^∘}{π}≈57.3^∘ \end{align}\]

Run across Figure \(\PageIndex{12}\). Note that when an bending is described without a specific unit, it refers to radian measure. For example, an angle measure of 3 indicates iii radians. In fact, radian mensurate is dimensionless, since it is the quotient of a length (circumference) divided past a length (radius) and the length units abolish out.

Effigy \(\PageIndex{12}\): The bending \(t\) sweeps out a mensurate of ane radian. Note that the length of the intercepted arc is the same as the length of the radius of the circumvolve.

Relating Arc Lengths to Radius

An arc length \(s\) is the length of the curve forth the arc. Simply equally the full circumference of a circumvolve ever has a constant ratio to the radius, the arc length produced past whatever given angle besides has a abiding relation to the radius, regardless of the length of the radius.

This ratio, called the radian measure out, is the same regardless of the radius of the circle—it depends only on the angle. This belongings allows us to ascertain a measure of any angle as the ratio of the arc length s s to the radius \(r\). Run across Figure \(\PageIndex{xiii}\).

\[\begin{align} south &=rθ \\ θ &=\dfrac{due south}{r} \end{align}\]

If \( southward=r\), then \(θ=\frac{r}{r}= 1 \text{ radian.}\)

Effigy \(\PageIndex{xiii}\): (a) In an angle of 1 radian, the arc length \(due south\) equals the radius \(r.\) (b) An angle of ii radians has an arc length \(s=2r\). (c) A full revolution is 2π or about 6.28 radians.

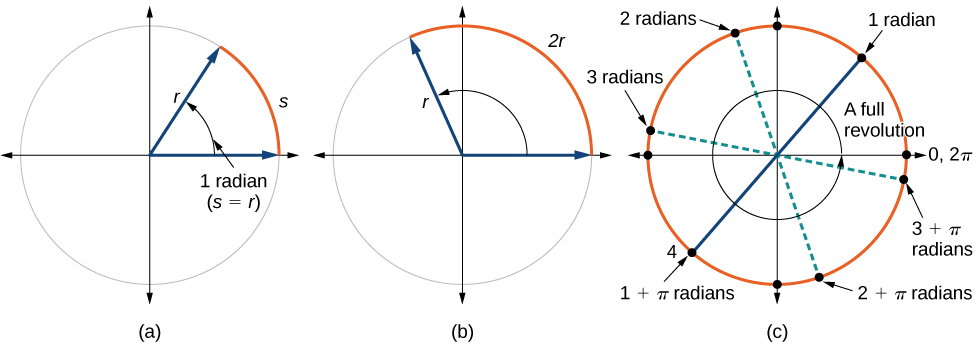
To elaborate on this idea, consider 2 circles, 1 with radius ii and the other with radius 3. Recall the circumference of a circumvolve is \(C=2πr\),where \(r\) is the radius. The smaller circle then has circumference \(2π(2)=4π\) and the larger has circumference \(2π(iii)=6π\). At present we describe a 45° angle on the two circles, as in Figure \(\PageIndex{14}\).

Effigy \(\PageIndex{14}\): A 45° angle contains i-eighth of the circumference of a circle, regardless of the radius.

Detect what happens if we detect the ratio of the arc length divided by the radius of the circle.

\[\brainstorm{marshal} \text{Smaller circle: } \dfrac{\frac{1}{2}π}{2} & =\dfrac{one}{4}π \\[2mm] \text{Larger circumvolve: } \dfrac{\frac{3}{iv}π}{iii} & =\dfrac{1}{four}π \end{marshal}\]

Since both ratios are \(\frac{1}{4}π\), the angle measures of both circles are the same, even though the arc length and radius differ.

RADIANS

1 radian is the measure of the central bending of a circle such that the length of the arc betwixt the initial side and the last side is equal to the radius of the circumvolve. A full revolution (360°) equals \(two\pi\) radians. A half revolution (180°) is equivalent to \(\pi\) radians.

The radian measure of an angle is the ratio of the length of the arc subtended by the bending to the radius of the circle. In other words, if \(s\) is the length of an arc of a circle, and \(r\) is the radius of the circle, and so the cardinal angle containing that arc measures \(\frac{s}{r}\) radians. In a circle of radius 1, the radian mensurate corresponds to the length of the arc.

A measure of ane radian looks to be about sixty°. Is that correct?

Yep. Information technology is approximately 57.3°. Because \(2π\) radians equals 360°, \(1\) radian equals \(\frac{360°}{2π}≈57.3°\).

Using Radians

Because radian measure is the ratio of two lengths, information technology is a unitless measure out. For example, in Figure \(\PageIndex{xiv}\), suppose the radius were 2 inches and the distance along the arc were too two inches. When we calculate the radian measure of the angle, the "inches" cancel, and we have a result without units. Therefore, information technology is not necessary to write the characterization "radians" afterward a radian measure, and if nosotros encounter an angle that is not labeled with "degrees" or the degree symbol, we can presume that it is a radian measure.

Considering the most basic case, the unit circumvolve (a circle with radius 1), nosotros know that 1 rotation equals 360 degrees, 360°. We can also track one rotation around a circle by finding the circumference, \(C=2πr\), and for the unit circle \(C=2π.\) These two different ways to rotate around a circle requite united states a way to convert from degrees to radians.

\[\brainstorm{array}{clll} 1 \text{rotation } & =360° & =2π & \text{radians} \\[2mm] \dfrac{i}{2} \text{rotation } & =180° & =π & \text{radians} \\[2mm] \dfrac{1}{iv} \text{rotation } & =90° & =\dfrac{π}{ii} & \text{radians} \end{assortment}\]

Identifying Special Angles Measured in Radians

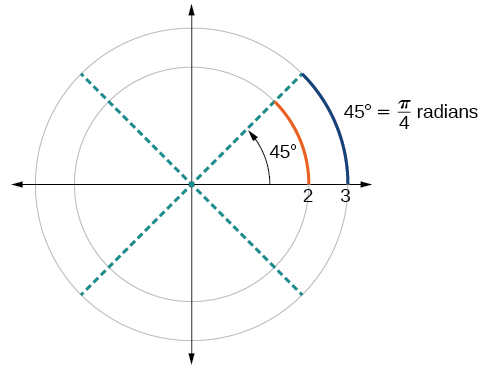
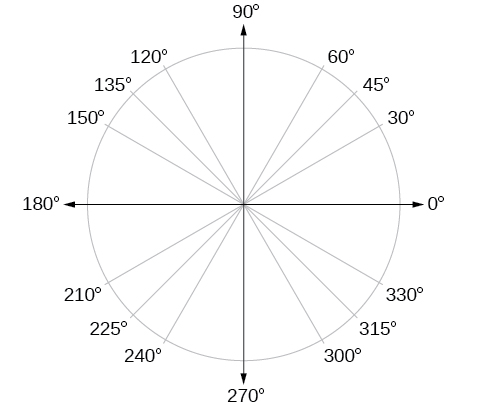
In addition to knowing the measurements in degrees and radians of a quarter revolution, a half revolution, and a full revolution, in that location are other oft encountered angles in one revolution of a circle with which we should be familiar. Information technology is common to see multiples of 30, 45, 60, and 90 degrees. These values are shown in Figure \(\PageIndex{15}\). Memorizing these angles will be very useful as we study the properties associated with angles.

Figure \(\PageIndex{fifteen}\): Commonly encountered angles measured in degrees

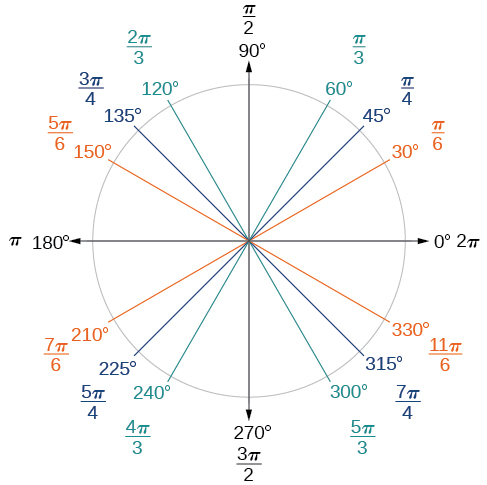
At present, we can list the corresponding radian values for the common measures of a circle corresponding to those listed in Figure \(\PageIndex{15}\), which are shown in Figure \(\PageIndex{16}\). Exist sure you tin verify each of these measures.

Figure \(\PageIndex{xvi}\): Commonly encountered angles measured in radians

Example \(\PageIndex{2}\): Finding a Radian Measure

Find the radian measure of one-tertiary of a full rotation.

Solution

For any circle, the arc length forth such a rotation would be ane-third of the circumference. Nosotros know that

\[1 \text{ rotation}=2πr\]

And so,

\[\begin{marshal}s &= \dfrac{1}{3}(2πr) \\[2mm] &=\dfrac{2πr}{3} \stop{align}\]

The radian measure would be the arc length divided by the radius.

\[\begin{align} \text{radian measure} & = \dfrac{\frac{2πr}{iii}}{r} \\[2mm] &= \dfrac{2πr}{3r} \\[2mm] & = \dfrac{2π}{3} \end{align}\]

\(\PageIndex{2}\)

Find the radian measure out of three-fourths of a full rotation.

Solution

\[\dfrac{3π}{2}\]

Converting between Radians and Degrees

Because degrees and radians both measure angles, we need to be able to convert between them. We can hands do so using a proportion.

\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]

This proportion shows that the measure of angle \(θ\) in degrees divided by 180 equals the measure of angle \(θ\) in radians divided by \(π.\) Or, phrased another way, degrees is to 180 equally radians is to \(π\). Nosotros tin use fact that \(180^∘=\pi\) radians to convert between degree and radian measure.

CONVERTING BETWEEN RADIANS AND DEGREES

To catechumen an angle from radian measure to caste measure, multiply the value past the fraction \(\dfrac{180^∘}{\pi}\) and simplify

To catechumen an bending from degree measure to radian measure, multiply the value past the fraction \(\dfrac{\pi}{180^∘}\) and simplify

Example \(\PageIndex{iii}\): Converting Radians to Degrees

Convert each radian measure to degrees.

1. \(\frac{π}{6}\)
2. 3

Solution

i. Because nosotros are given radians and we want degrees, nosotros should multiply by \(\dfrac{180^∘}{\pi}\) and simplify

\[ (\frac{π}{six}) (\dfrac{180^∘}{\pi}) = \dfrac{\pi180^∘}{half-dozen\pi} = \dfrac{180^∘}{half-dozen} = 30^∘ \]

two. Because we are given radians and we desire degrees, we should multiply by \(\dfrac{180^∘}{\pi}\) and simplify

\[ 3 (\dfrac{180^∘}{\pi}) = \dfrac{three*180^∘}{\pi} = \dfrac{540^∘}{\pi} ≈ 171.89^∘ \]

\(\PageIndex{3}\)

Catechumen \(−\frac{3π}{4}\) radians to degrees.

Solution

−135°

Example \(\PageIndex{4}\): Converting Degrees to Radians

Catechumen \(15\) degrees to radians.

Solution

In this example, we first with degrees and want radians, then we multiply past \(\dfrac{\pi}{180^∘}\) and simplify

\[ xv * (\dfrac{\pi}{180^∘}) = \dfrac{15\pi}{180^∘} = \dfrac{\pi}{12} \]

\(\PageIndex{4}\)

Convert 126° to radians.

Solution

\(\frac{7π}{10}\)

Finding Coterminal Angles

Converting betwixt degrees and radians can make working with angles easier in some applications. For other applications, we may need some other type of conversion. Negative angles and angles greater than a full revolution are more than bad-mannered to work with than those in the range of 0° to 360°, or 0 to \(2π\). Information technology would be convenient to supersede those out-of-range angles with a respective angle inside the range of a single revolution.

Information technology is possible for more than one angle to have the same terminal side. Await at Figure \(\PageIndex{17}\). The angle of 140° is a positive angle, measured counterclockwise. The angle of –220° is a negative angle, measured clockwise. But both angles have the same terminal side. If two angles in standard position have the same terminal side, they are coterminal angles. Every bending greater than 360° or less than 0° is coterminal with an angle between 0° and 360°, and information technology is oftentimes more user-friendly to find the coterminal angle inside the range of 0° to 360° than to work with an bending that is exterior that range.

Figure \(\PageIndex{17}\): An angle of 140° and an angle of –220° are coterminal angles.

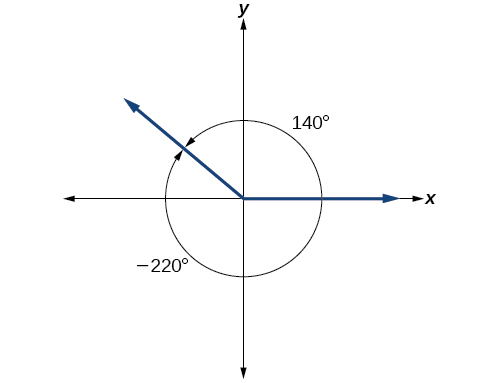
Any angle has infinitely many coterminal angles because each time we add together 360° to that angle—or subtract 360° from it—the resulting value has a concluding side in the same location. For example, 100° and 460° are coterminal for this reason, equally is −260°. Recognizing that any angle has infinitely many coterminal angles explains the repetitive shape in the graphs of trigonometric functions.

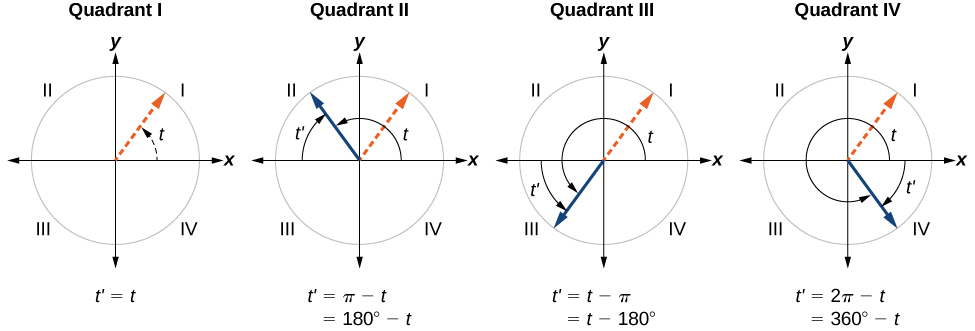
An angle'south reference angle is the measure out of the smallest, positive, acute angle \(t\) formed by the concluding side of the angle \(t\) and the horizontal centrality. Thus positive reference angles have last sides that lie in the commencement quadrant and can be used every bit models for angles in other quadrants. See Figure \(\PageIndex{18}\) for examples of reference angles for angles in unlike quadrants. In the effigy, \(t\) is the given angle and \(t'\) is the reference angle.

Figure \(\PageIndex{18}\)

COTERMINAL AND REFERENCE ANGLES

• Coterminal angles are ii angles in standard position that have the same terminal side.
• An angle's reference angle is the size of the smallest acute angle, \(t′\), formed by the final side of the bending \(t\) and the horizontal centrality.

Given an angle greater than 360°, notice a coterminal bending betwixt 0° and 360°

1. Subtract 360° from the given angle.
2. If the upshot is still greater than 360°, subtract 360° again till the result is between 0° and 360°.
3. The resulting angle is coterminal with the original angle.

Case \(\PageIndex{5}\): Finding an Angle Coterminal with an Angle of Measure Greater Than 360°

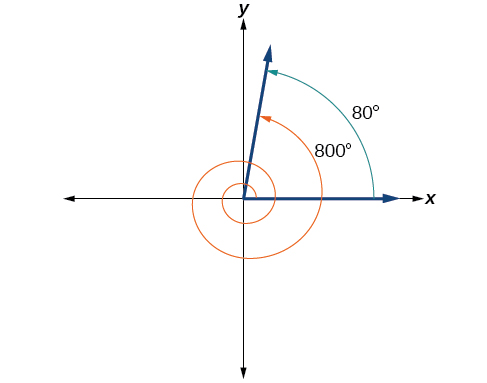
Find the least positive angle θ that is coterminal with an angle measuring 800°, where \(0°≤θ<360°\).

Solution

An angle with mensurate 800° is coterminal with an angle with measure 800 − 360 = 440°, simply 440° is still greater than 360°, so nosotros decrease 360° again to find another coterminal bending: 440 − 360 = lxxx°.

The angle \(θ=80°\) is coterminal with 800°. To put it some other way, 800° equals fourscore° plus two full rotations, as shown in Figure \(\PageIndex{19}\).

Effigy \(\PageIndex{xix}\)

\(\PageIndex{5}\)

Discover an angle \(α\) that is coterminal with an angle measuring 870°, where \(0°≤α<360°\).

Solution

\(α=150°\)

Given an angle with measure less than 0°, find a coterminal angle having a measure betwixt 0° and 360°.

1. Add together 360° to the given bending.
2. If the result is nevertheless less than 0°, add 360° again until the result is betwixt 0° and 360°.
3. The resulting angle is coterminal with the original angle.

Example \(\PageIndex{6}\): Finding an Angle Coterminal with an Angle Measuring Less Than 0°

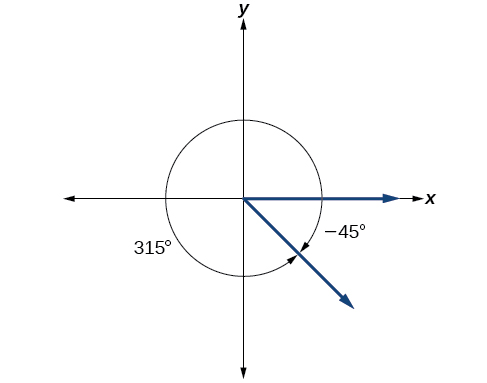
Show the angle with measure −45° on a circle and find a positive coterminal angle α such that 0° ≤ α < 360°.

Solution

Since 45° is half of xc°, we can start at the positive horizontal axis and mensurate clockwise half of a 90° angle.

Considering we can find coterminal angles by calculation or subtracting a total rotation of 360°, nosotros tin notice a positive coterminal angle here by calculation 360°:

\[−45°+360°=315°\]

We tin can then bear witness the angle on a circle, as in Figure \(\PageIndex{20}\).

Effigy \(\PageIndex{20}\)

\(\PageIndex{6}\)

Observe an angle β that is coterminal with an bending measuring −300° such that \(0°≤β<360°\).

Solution

\(β=60°\)

Finding Coterminal Angles Measured in Radians

We can observe coterminal angles measured in radians in much the same way as we have found them using degrees. In both cases, nosotros notice coterminal angles by adding or subtracting i or more full rotations.

Given an bending greater than \(ii\pi\), discover a coterminal angle between 0 and \(two\pi\).

1. Decrease \(2π\) from the given angle.
2. If the result is withal greater than \(2π\), subtract \(2π\) once again until the result is between \(0\) and \(2π\).
3. The resulting angle is coterminal with the original angle.

Example \(\PageIndex{7}\): Finding Coterminal Angles Using Radians

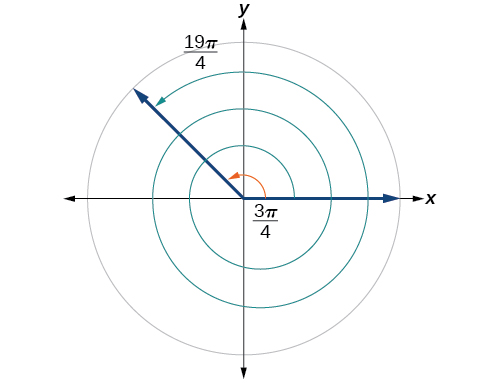
Detect an angle \(β\) that is coterminal with \(\frac{19π}{4}\), where \(0≤β<2π.\)

Solution

When working in degrees, we found coterminal angles by adding or subtracting 360 degrees, a full rotation. Besides, in radians, we tin can find coterminal angles by adding or subtracting total rotations of \(2π\) radians:

\[\begin{marshal} \dfrac{19π}{iv}−2π & =\dfrac{19π}{4}−\dfrac{8π}{4} \\ &=\dfrac{11π}{iv} \terminate{marshal}\]

The angle \(\frac{11π}{4}\) is coterminal, but not less than \(2π\), so nosotros subtract another rotation:

\[\begin{align} \dfrac{11π}{4}−2π &= \dfrac{11π}{four}−\dfrac{8π}{4} \\ &= \dfrac{3π}{4} \finish{align}\]

The angle \(\frac{3π}{4}\) is coterminal with \(\frac{19π}{four}\), as shown in Figure \(\PageIndex{21}\).

Figure \(\PageIndex{21}\)

\(\PageIndex{vii}\)

Notice an bending of measure out \(θ\) that is coterminal with an angle of measure out \(−\frac{17π}{half dozen}\) where \(0≤θ<2π.\)

Solution

\(\frac{7π}{vi}\)

Determining the Length of an Arc

Retrieve that the radian mensurate \(θ\) of an angle was divers as the ratio of the arc length \(s\) of a round arc to the radius \(r\) of the circle, \(θ=\frac{southward}{r}\). From this relationship, we tin find arc length along a circle, given an angle.

ARC LENGTH ON A Circumvolve

In a circle of radius r, the length of an arc \(due south\) subtended past an angle with measure out \(θ\) in radians, shown in Figure \(\PageIndex{22}\), is

\[south=rθ\]

Figure \(\PageIndex{22}\)

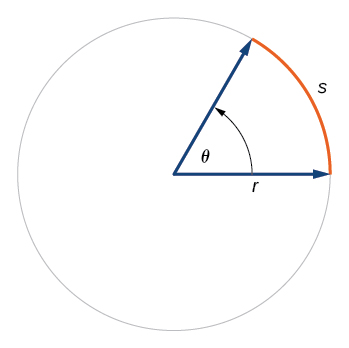
Given a circle of radius \(r,\) calculate the length \(south\) of the arc subtended by a given angle of mensurate \(θ\).

1. If necessary, convert \(θ\) to radians.
2. Multiply the radius \(r\) by the radian measure of \(θ:southward=rθ\).

Example \(\PageIndex{8}\): Finding the Length of an Arc

Presume the orbit of Mercury effectually the sun is a perfect circle. Mercury is approximately 36 one thousand thousand miles from the sun.

1. In ane Earth 24-hour interval, Mercury completes 0.0114 of its full revolution. How many miles does it travel in 1 day?
2. Utilize your reply from function (a) to determine the radian measure for Mercury's motion in one Earth twenty-four hours.

Solution

1. Let'south begin by finding the circumference of Mercury'southward orbit.

   \[\begin{align} C &=2πr \\ &=2π(\text{36 meg miles}) \\ &≈226 \text{ million miles} \stop{marshal}\]

   Since Mercury completes 0.0114 of its total revolution in ane Earth day, nosotros tin now detect the distance traveled:

   \[(0.0114)226 \text{ million miles} = two.58 \text{ million miles}\]

2. Now, we convert to radians:

   \[\begin{align} \text{radian} & = \dfrac{\text{arc length}}{\text{radius}} \\ &= \dfrac{two.58 \text{ million miles}}{36 \text{ million miles}} \\ & =0.0717 \end{marshal} \]

\(\PageIndex{viii}\)

Find the arc length along a circle of radius 10 units subtended past an angle of 215°.

Solution

\[\dfrac{215π}{18}=37.525 \text{ units} \]

Finding the Surface area of a Sector of a Circumvolve

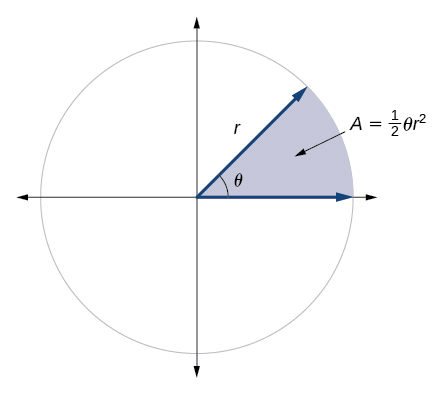
In add-on to arc length, nosotros can also use angles to notice the area of a sector of a circle. A sector is a region of a circle bounded by two radii and the intercepted arc, like a slice of pizza or pie. Recall that the area of a circle with radius \(r\) tin be found using the formula \(A=πr^two\). If the two radii grade an bending of \(θ\), measured in radians, and then \(\frac{θ}{2π}\) is the ratio of the angle measure to the measure of a full rotation and is too, therefore, the ratio of the area of the sector to the area of the circle. Thus, the area of a sector is the fraction \(\frac{θ}{2π}\) multiplied past the entire area. (Always remember that this formula only applies if \(θ\) is in radians.)

\[\brainstorm{marshal} \text{Surface area of sector} & =(\dfrac{θ}{2π})πr^2 \\ &=\dfrac{θπr^ii}{2π} \\ & =\dfrac{1}{two}θr^2 \end{align}\]

AREA OF A SECTOR

The area of a sector of a circumvolve with radius \(r\) subtended by an angle \(θ\), measured in radians, is

\[A=\dfrac{one}{2}θr^2\]

Come across Effigy \(\PageIndex{23}\).

Figure \(\PageIndex{23}\): The expanse of the sector equals half the square of the radius times the primal bending measured in radians.

Given a circle of radius \(r,\) find the area of a sector defined past a given angle \(θ.\)

1. If necessary, convert \(θ\) to radians.
2. Multiply half the radian measure of \(θ\) by the foursquare of the radius \(r: A=\frac{1}{2}θr^2.\)

Example \(\PageIndex{nine}\): Finding the Expanse of a Sector

An automatic backyard sprinkler sprays a altitude of 20 feet while rotating 30 degrees, equally shown in Effigy \(\PageIndex{24}\). What is the area of the sector of grass the sprinkler waters?

Figure \(\PageIndex{24}\): The sprinkler sprays 20 ft within an arc of 30°.

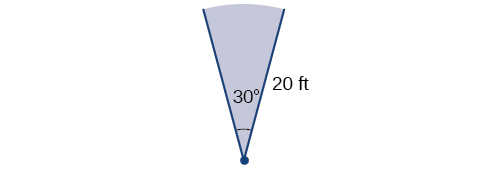
Solution

Showtime, we need to convert the angle measure into radians. Because xxx degrees is one of our special angles, we already know the equivalent radian measure, but we can likewise convert:

\[\begin{marshal} \text{thirty degrees} &=thirty⋅\frac{π}{180} \\ &=\frac{π}{vi} \text{ radians} \stop{align}\]

The expanse of the sector is then

\[\brainstorm{align} \text{Expanse} &= \dfrac{1}{2}(\dfrac{π}{vi})(20)^2 \\ & ≈104.72 \end{align}\]

So the area is about \(\mathrm{104.72 \; ft^2}\).

\(\PageIndex{9}\)

In central pivot irrigation, a large irrigation piping on wheels rotates around a center point. A farmer has a central pivot arrangement with a radius of 400 meters. If water restrictions only allow her to water 150 k square meters a mean solar day, what angle should she set the arrangement to cover? Write the answer in radian mensurate to two decimal places.

Solution

ane.88

Key Concepts

• An angle is formed from the union of two rays, by keeping the initial side fixed and rotating the terminal side. The amount of rotation determines the measure of the bending.
• An angle is in standard position if its vertex is at the origin and its initial side lies along the positive x-axis. A positive angle is measured counterclockwise from the initial side and a negative angle is measured clockwise.
• To depict an angle in standard position, draw the initial side along the positive 10-axis and and so place the terminal side according to the fraction of a full rotation the bending represents. Encounter Example.
• In add-on to degrees, the mensurate of an angle can be described in radians. Come across Example.
• To convert between degrees and radians, use the proportion \(\frac{θ}{180}=\frac{θ^R}{π}\). See Example and Example.
• Two angles that take the aforementioned concluding side are called coterminal angles.
• We can detect coterminal angles by adding or subtracting 360° or \(2π\). Run across Example and Example.
• Coterminal angles tin can exist found using radians just as they are for degrees. See Example.
• The length of a circular arc is a fraction of the circumference of the entire circle. Run into Example.
• The expanse of sector is a fraction of the expanse of the entire circle. Encounter Example.

Glossary

angle

the union of two rays having a common endpoint

arc length

the length of the bend formed by an arc

area of a sector

area of a portion of a circle bordered by two radii and the intercepted arc; the fraction \(\frac{θ}{2π}\) multiplied by the area of the entire circle

coterminal angles

clarification of positive and negative angles in standard position sharing the same terminal side

caste

a unit of measure describing the size of an angle as one-360th of a full revolution of a circumvolve

initial side

the side of an angle from which rotation begins

measure of an angle

the amount of rotation from the initial side to the final side

negative angle

description of an angle measured clockwise from the positive x-centrality

positive angle

description of an angle measured counterclockwise from the positive x-axis

quadrantal angle

an angle whose last side lies on an centrality

radian measure

the ratio of the arc length formed by an angle divided by the radius of the circumvolve

radian

the measure of a central angle of a circumvolve that intercepts an arc equal in length to the radius of that circle

ray

1 point on a line and all points extending in i direction from that point; one side of an angle

reference angle

the mensurate of the acute angle formed past the terminal side of the bending and the horizontal axis

standard position

the position of an bending having the vertex at the origin and the initial side along the positive x-axis

final side

the side of an angle at which rotation ends

vertex

the common endpoint of two rays that class an angle

Standard Position Of An Angle,

Source: https://math.libretexts.org/Courses/Reedley_College/Trigonometry/01%3A_The_Six_Trigonometric_Functions/1.01%3A_Angles

Posted by: boothfrass1954.blogspot.com

Share this post